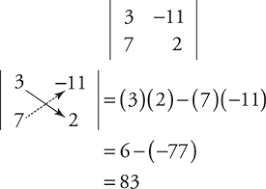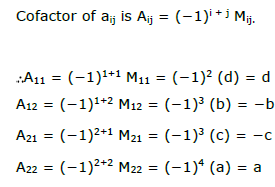ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam