
ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam

ICOME
Indian Competition Oriented Mathematical Exam


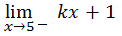 =
= 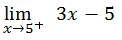 = 4k + 1
= 4k + 1 
 ,
,  and
and  are coplaner .
are coplaner .

 ] = 0
] = 0 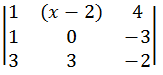 = 0
= 0