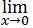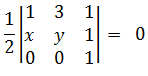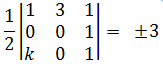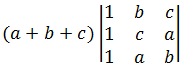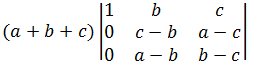Section C
Solution. 13 .
Let f(x) = asin
π/2
(x + 1), x ≤ 0
tan x - sin x/x3
, x > 0
is continuous at x = 0
∴ LHL = RHL = f(0)
Here, LHL =
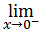
a sin
π/2
(x+1)
⇒ LHL
=

a sin
π/2
(-h+1)
[put x = 0 - h;when x →0
-, then h → 0]
a sin
π/2
= a
f(0) = a sin
π/2
= a
Now,we need to evaluate RHL at x = a .
[∵ LHL = f(0) = a and from this, we can't find the value of a]
Here,RHL =
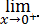
tan x - sin x/x3
⇒ RHL =

tan h - sin h/h3
[put x = 0 + h = h; whenx → 0
+,then h → 0]
=

=

sin h - sin h cos h/h3 cos h
=

sin h(1 - cos h)/h3 cos h
=

sin h/h
.

1 - cos h/h2
.

1/cos h
= 1 x

1 - cos h/h2
x 1
[∵

sin h/h
and

1/cos h
=
1/cos 0
=
1/1
= 1]
=

1 - cos h/h2
=

2 sin2(h/2)/h2
[∵ 1 - cos x = 2 sin
2 (x/2)]
=

2 x sin2(h/2)/(h2/4) x 4
=

(2/4) x
sin2(h/2)/h2
= (1/2) x

(
sin(h/2)/h/2
)
2
= (1/2) x 1
[∵
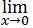
sin x/x
]
∴ RHL =
1/2
From Eq. (i) we have LHL = RHL
a =
1/2
Solution. 14 . cos(cos
-11/√(x2 + 1)
)
= sin(sin
-14/5
)
1/√(x2 + 1)
=
4/5
on squaring both sides, we get
16x
2 + 16 = 25
16x
2 = 9
x = ±
3/4
∴ cos(cos
-1x) = x and sin (sin
-1x) = x , x∈[-1,1]
Solution. 15 . Given, f(x) = lxl + x and g(x) = lxl - x for all x ∈ R
⇒ f(x) = (x + x, x ≥ 0 )
(- x + x , x < 0)
and ⇒ g(x) = x - x, x ≥ 0
- x - x,x < 0
⇒ f(x) = 2x, x ≥ 0
0,x < 0
and g(x) = 0 , x ≥ 0
-2x , x < 0
Thus, for x ≥ 0, gof(X) = g(2x) = 0
and for x < 0, gof = g(0)
⇒ gof(x) = 0, all x ∈ R
Similarly , for x ≥ 0, fog(x) = f(0) = 0
and for x < 0 , fog (x) = f(-2x) = 2(-2x) = -4x
⇒ fog(x) = 0, x ≥ 0
-4x, x < 0
Solution. 16 .
= sin
-1(
1/3
) + sin
-1
(
2√2/3
)
= tan
-11/2√2
+ tan
-12√2
= tan
-11/2√2
+ 2√2/
1 - 1/2√2
. 2√2 =
π/2
∴ tan
-1 x + tan
-1y = tan
-1
x+y/1 - xy
Solution . 17Let P(x,y) be any point on the line joining A(1,3) and B(0,0)
Then area of (▵APB) = 0
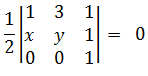
1(y) - 3(x) + 1(0) = 0
y - 3x = 0
y = 3x
Since area of triangle ABC = 3 sq units
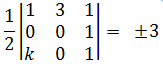
1(0) - 3(-k) + 1(0) = ± 6
3k = ±6
k = ± 2
Solution . 18Solve this with the help of row and column transformation
So,Apply C
1 →
C
1 + C
2 + C
3 =

On taking common (a+b+c) from C
1
=
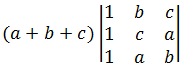
Now apply R
2 → R
2 - R
1 and R
3 → R
3
- R
1
=
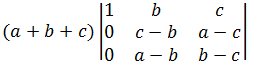
Now expand with respect to C
1 = (a+b+c)[(c-b)(b-c)-(a-b)(a-c)]
= (a+b+c)(-1)[(b-c)
2+ (a-b)(a-c)]
= -(a+b+c)[b
2 + c
2 - 2bc + a
2 - ac - ba + bc]
= (a+b+c)[a
2 + b
2 + c
2 - ac - ab - bc]
multiply and divide by 2
=
-(a+b+c)/2
[2a
2 + 2b
2 + 2c
2 -2ac - 2ab - 2bc]
→ -
1/2
(a+b+c)
[(a-c)
2 + (b-c)
2 + (c-a)
2] < 0
∴ a,b,c > 0 and a ≠ b ≠ c .
Solution . 19 This problem belongs to logarithmic differentiation, so take log both sides to get desired result
given x
y = e
x-yOn taking log both sides, we get
ylog
ex = (x - y)log
ee
⇒ ylog
ex = x - y [∵log
ee = 1]
⇒ y(1 + logx) = x ⇒ y =
x/1 + logx
On differentiating both
sides w.r.t. x, we get
dy/dx
=
(1 + logx)d/dx
(x) -
d/dx
(1 + logx)/
(1 + logx)2
∵
d/dx
(
v/u
) =
1 + logx - x.1/x
/(1 + logx)2 =
1 + log x - 1 /(1 + logx)2
Hence,
dy/dx
=
log x/(1 + logx)2
Also,it can be written as
dy/dx
=
log x /(logee + logx)2
dy/dx
=
log x /(log(ex))2
Solution . 20 Given differential equation is
(x log lxl)
dy/dx
+ y = 2 loglxl
On dividing both
sides by x log lxl, we get
dy/dx
+
y/x loglxl
=
2/x
which is a linear differential
equation of the form
dy/dx
+ Py = Q
On comparing, we get
P =
1/x loglxl
and Q =
2/x
∴ IF = e
∫(1/xloglxl)dx
= log
logllog xl [put loglxl = t
1/x
dx = dt
∴ ∫
1/x loglxl
dx =
∫
dt/t
= logltl = log llog x l ]
= log x [∵ e
log lxl
= x]
The solution of linear differential equation is given by
y x IF = ∫ Q x IF dx + C
∴ y x loglxl
= ∫ 2/x loglxl dx
⇒ y log lxl = log lxl ∫2/x dx
- ∫ [d/dx (log lxl)∫2/x dx]dx
[using integration by parts]
⇒ y log lxl = log lxl.2log lxl - ∫ 1/x . 2log lxl dx
[∴ ∫ 1/x dx = log lxl + C]
⇒ y log lxl = 2(log lxl)
2 - 2 ∫ (log lxl)/x dx
⇒ y log lxl = 2(log lxl)
2 -
2(log lxl)2/2
+ C
[put log lxl = t ⇒
1/x
dx = dt]
∴ ∫
log lxl/x
dx = ∫
t dt =
t2/2
=
(log lxl)2/2
]
y = 2(log lxl) - (log lxl) +
C/log lxl
[dividing both sides by log lxl]
y = log lxl +
C/log lxl
which is the required solution .
Solution . 21Let x and y denotes table and chair respectively
So, formulation of this problem
z = 20x + 30y
subject to: 4x + 5y ≥ 200
3x + 4y ≤ 240
y ≥ 20
x, y ≥ 20
Now, Solve this problem graphically. first of all draw the straight lines for all the given
inequalities.
4x + 5y = 200
put x = 0 , y = 0
y = 0=40 , x = 50
(0,40) (50,0)
3x + 4y = 240
put x = 0 , y = 0
(0,60) y = 60 , x = 80 (80,0)
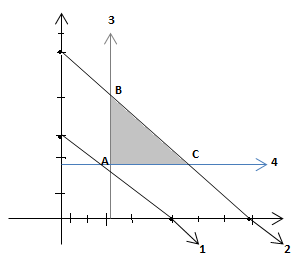
Solve equation 3 and 4, to get point A
Point A (30,20)
Solve equation 2 and 3, to get point B
3x + 4y = 240
x = 30
3(30) + 4y = 240
4y = 150
y = 37.5
Points B (30,37.5)
Solve equation 2 and 4, to get point C
3x + 4y = 240
y = 20
3x + 4(20) = 240
x = 53.4
Point C(53.4,20)
Now find z for all points
Z
A = 20(30) + 30(20) = 1200
Z
B = 20(30) + 30(37.5) = 1725
Z
C = 20(53.4) + 30(20) = 1668
Optimal solution is Rs.1200 at point A (30,20)
Solution . 22Let P = probability of success and q = probability of failure and x be a random variable that denote the number of
sucess in 6 trials .
x follows binomial distribution , having parameters n = 6, p
∴P(x = x) = 6C
x .
P
x . q
n-x x = 0,1,2,3,4,5,6
As per question P(x = 4) =
1/4
P(x = 2)
4P(x = 4) = P(x = 2)
4(6C
4P
4q
2) = 6C
2P
2q
4 (∵nc
x = nc
n-x)
4P
2 = q
24P
2 = (1 - P)
2
4P
2 = 1 + P
2 - 2P
3P
2 + 2P - 1 = 0
3P
2 + 3P - P - 1 = 0
3P(P + 1) - 1(P + 1) = 0
(3P - 1)(P + 1) = 0
P =
1/3
, -1
P =
1/3
( p = -1,
Probability can't be negative.)
Solution . 23 Let us define the events
E
1 = a red and a black ball is transferred
E
2 = two red balls are transferred.
E
3 = two black balls are transferred.
A = ball drawn from bag B is red .
then P(E
1) =
4C1 x 4C1 /
8C2
=
4/7
P(E
2) =
4C2/8C2
=
3/14
P(E
3) =
4C2/8C2
=
3/14
P(A/E
1) =
4/10
P(A/E
2) =
5/10
P(A/E
3) =
7/10
P(E
2/A) =
P(A/E2).P(E2)/
P(A/E1).P(E1) + P(A/E2).P(E2) + P(A/E3) . P(E3)
=
(5/10) x (3/14)/4/10 x 4/7 + 5/10 x 3/14 + 7/10 x 3/14
=
15/68


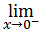 a sin
a sin a sin
a sin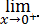













 (2/4) x
(2/4) x  (
(