Section D
Solution.24
Let I =  (2 log lsin xl - loglsin 2xl)dx
(2 log lsin xl - loglsin 2xl)dx
⇒ I =  (2 log lsin xl - logl2sinx cos xl)dx
(2 log lsin xl - logl2sinx cos xl)dx
[∵ sin x > 0 for 0 < x <
π/2
and
sin 2x = 2sinx cosx]
⇒ I =  [2 log(sin x) - (log 2 + log(sin x) + log(cos x)]dx
[2 log(sin x) - (log 2 + log(sin x) + log(cos x)]dx
[∵ log(mnp) = log m + log n + log p]
⇒ I =  [2 log(sinx) - log 2 - log(sin x) - log(cos x)]dx
[2 log(sinx) - log 2 - log(sin x) - log(cos x)]dx
⇒ I =  (log(sin x) - log 2 -log(cos x))dx
(log(sin x) - log 2 -log(cos x))dx
⇒ I =  log(sin x)dx -
log(sin x)dx -
 log 2 dx -
log 2 dx -  log(cos x) dx
log(cos x) dx
⇒ I =  log cos x dx - log 2 [
log cos x dx - log 2 [
π/2
- 0] -  log cos x dx
log cos x dx
∴ I = - π/2
log 2
Solution.25
Let C denotes the curved surface area , r be the radius of base, h be the height aand V be the volume
of right circular cone.
To show, h = √2r
We know that, volume of cone is given by
V= 1/3
πr2h ⇒ h =
3V/πr2
Also,the curved surface area of cone is given by C = πrl, where l = √(r2 + h2) is the slant height of cone.
∴ C = πr√(r2 + h2)
On squaring both sides, we get
C2 = π2r2
(r2 + h2)⇒ C2 = π2r4 + π2r2h2
Let C2 = Z
Then Z = π2r4 + π2r2h2
⇒
Z = π2r4 + π2r2(3V/πr2
)2
⇒ Z = π2r4 + π2r29V2/
π2r4
⇒ Z = π2r4 +
9V2/r4
On differentiating both sides w.r.t.r, we get
dZ/dr
= 4π2r3 - 18V2/r3
For maxima or minima put dZ/dr
= 0
⇒ 4π2r3 - 18V2/r3
= 0
⇒ 4π2r3 = 18V2/r3
⇒ 4π2r3 = 18 (1/3
πr2h )2
[∵V = 1/3
πr2h ]
⇒ 4π2r6 = 18 x 1/9
π2r4h2
⇒ 4π2r6 = 2π2r4h2
⇒ 2r2 = h2
∴ h = √2r
Hence , height = √2 x (radius of base)
Also, d2Z/dr2
=
d/dr
(
dZ/dr
) = d/dr
(4π2r3 - 18V2/r3
)
= 12π2r2 + 54V2/r4
)
d2Z/dr2
=
12π2r2 + 54V2/r4
> 0
Solution.26
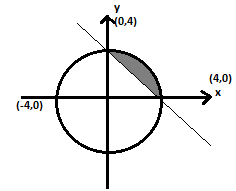
The region has a circle with equation
x2 + y2 = 16 (circle)
x + y = 4 (line)
Circle has center (0,0) and radius is 4, wide line has equal intercept on x and y axis that is 4.
Point of intersection is
calculated as follows
x2 + y2 = 16
x2 + + (4 - x)2 = 16
x2 + 16 + x2 - 8x = 16
2x2 - 8x = 0
2x(x - 4) = 0
x = 0 or 4
when x = 0, then y = 4
and when x = 4, then y = 0
So the points of intersection are (0,4) and (4,0) on drawing the graph, area
of shaded region is to be calculated
So, required area = 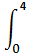 (y circle - y line) dx
(y circle - y line) dx
= 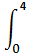 [
[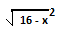 - (4 - x)]dx
- (4 - x)]dx
= 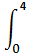 (
(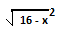 )dx
-
)dx
- 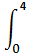 (4 - x)dx
(4 - x)dx
= [x/2
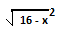 +
+ 16/2
sin-1
x/4
] - [4x - x2
/2
]
= [0 + 8sin-1(1) - 0 - 8sin-1(0)] -
[16 - 16/2
- 0]
=
= 8 . π/2
- 8
= 8(π
/2
- 1)
= 8
(π - 2/2
= 4(π - 2)sq. unit
Solution.27
Given differential equation is
x dy/dx
sin(y/x
) = y sin (
y/x
) - x
⇒ dy/dx
=
y/x
-
[dividing both sides by x sin (y/x
)]
Let F(x,y) = y/x
-
On replacing x by kx and y by ky both sides, we get
F (kx,ky) =
ky/kx
-
= k0 ( y/x
-
)
= k0 F(x,y)
So,given differential equation is homogeneous. On putting y = vx
⇒
dy/dx
= v + x
dy/dx
In equation (1) we get
V + x dy/dx
= V -
1/sin v
⇒
x dy/dx
= -
1/sin v
⇒ sin v dv = -
dx/x
On integrating both sides, we get
∫ sin v dv = ∫
dx/x
⇒ - cos v = - log lxl + C
⇒ - cos y/x
= - log lxl
+ C [put v = y/x
]
Also, given that x = 1,
when y = π/2
On putting x = 1and
y = π/2
In equation (ii), we get
- cos (π/2
) = log l1l + C
⇒ -0 = 0 + C ⇒ C = 0
On putting the value of C in equation (ii), we get
cos y/x
= log lxl
which is the required solution .
Solution.28
a→
= î + ĵ +k̂,b→
= 2î + 4ĵ -5k̂ and c→
= μî + 2ĵ +3k̂
Now, b
→ + c→ = 2î + 4ĵ
- 5k̂ + μî + 2ĵ + 3k̂
= (2 + μ)î + 6ĵ - 2k̂
∴
lb→ +
c→ l = √[(2 + μ)2 + (6)
2 + (-2)2]
= √[4 + μ2 + 4μ + 36 + 4]
= √(μ2
+ 4μ + 44)
The unit vector along b→ +
c→
b→ +
c→/
lb→ +
c→l
=
(2 + μ)î + 6ĵ - 2k̂/
√(μ2 + 4μ + 44)
Now as given in question, scalar product of (î + ĵ +k̂)
with unit vector b→ +
c→ is 1.
(î + ĵ +k̂). b→ +
c→/
lb→ +
c→l
= 1
î + ĵ +k̂.(2 + μ)î + 6ĵ - 2k̂/
√(μ2 + 4μ + 44)
= 1
(2 + μ)1 + (6)1 + (-2)1/
√(μ2 + 4μ + 44)
= 1
(2 + μ) + 6 - 2/
√(μ2 + 4μ + 44)
= 1
μ + 6 = √(μ2 + 4μ + 44)
(μ + 6)2 = μ2 + 4μ + 44, squaring both sides we get,
μ2 + 36 + 12μ = μ2 + 4μ + 44
8μ = 8
μ = 1
So, the value of μ is 1.
Solution.29
Given equation of planes are
r→.(î - 2 ĵ + 3 k̂)
= 4 and
r→.(-2î -
ĵ + k̂) = - 5
On comparing these with
r→.
n→= d, now we get
n1→ = î-2ĵ+3k̂,
d1 = 4,
n2→ =
-2î + ĵ + k̂ and d2 = -5
Now, the equation of the plane which contains the intersection of the given plane is
r→.(n1→
+ μn2→) = d1
+ μd2
r→
.[î - 2ĵ + 3ĵ + μ(-2î + ĵ + k̂)] = 4 - 5μ
r→
.[(1-2μ)î + (-2 + μ)ĵ + (3 + μ)k̂] = 4 - 5μ -----(1)
Now it is given that intercept on X and Y axis are same
4 - 5μ/1 - 2μ
=
4 - 5μ/-2 + μ
On putting μ = 1 in equation (1), we get
r→.
[(1-2)î + (-2 + 1)ĵ + (3 + 1)k̂] = 4 - 5 x 1
r→
.(-î - ĵ + 4k̂) = -1
equation of plane.


 (2 log lsin xl - loglsin 2xl)dx
(2 log lsin xl - loglsin 2xl)dx (2 log lsin xl - logl2sinx cos xl)dx
(2 log lsin xl - logl2sinx cos xl)dx
 [2 log(sin x) - (log 2 + log(sin x) + log(cos x)]dx
[2 log(sin x) - (log 2 + log(sin x) + log(cos x)]dx [2 log(sinx) - log 2 - log(sin x) - log(cos x)]dx
[2 log(sinx) - log 2 - log(sin x) - log(cos x)]dx (log(sin x) - log 2 -log(cos x))dx
(log(sin x) - log 2 -log(cos x))dx log(sin x)dx -
log(sin x)dx -
 log 2 dx -
log 2 dx -  log(cos x) dx
log(cos x) dx log cos x dx - log 2 [
log cos x dx - log 2 [
 log cos x dx
log cos x dx

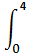 (y circle - y line) dx
(y circle - y line) dx
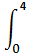 [
[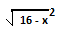 - (4 - x)]dx
- (4 - x)]dx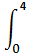 (
(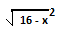 )dx
-
)dx
- 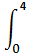 (4 - x)dx
(4 - x)dx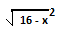 +
+