Section D
Solution.23
OR
Solution.23
Let the numerator of the fraction be x . Then,
∴ Fraction =
x
/2x + 1
⇒ Reciprocal of the fraction =
2x + 1/x
It is given that the sum of the
fraction and its reciprocal is216/21
x/2x + 1
+
2x + 1/x
=
216/21
x2 + (2x + 1)2/
x(2x + 1)
= 58/21
5x2 + 4x + 1/
2x2 + x
= 58/21
21 (5x2 + 4x + 1) = 58(2x2 + x)
105x2 + 84x + 21 = 116x2 + 58x
11x2 - 26x - 21 = 0
11x2 - 33x + 7x - 21 = 0
11x(x - 3) + 7(x -
3) = 0
(11x + 7)(x - 3) = 0
⇒ x = 3 , -
7/11
, ⇒ x = 3
Hence, fraction x/2x + 1
=
3/7
Solution.24
We have,
S1 = Sum of n terms of an A.P. with first term 1 and common difference 1
S1 = n/2
{2 x 1 +(n - 1) x 1}
= n/2
(n + 1)
S2 = Sum of n terms of an A.P. with first term 1 and common difference 2
S2 =
n/2
{2 x 1 +(n - 1) x 2} = n2
S3 = Sum of n terms of an A.P. with first term 1 and common difference 3
S3 = n/2
{2 x 1 +(n - 1) x 3}
= n/2
(3n - 1)
Now,S1 + S3 = n/2
(n + 1) + n/2
(3n - 1) = 2n2
and S2 = n2
Hence, S1 + S3 = 2S2
Solution.25
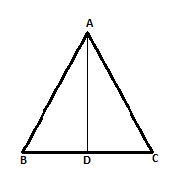
Let ABC be an equilateral triangle and AD ⊥ BC
In ∆ ADB and ∆ ADC, we have
AB = AC
∠B = ∠C
and , ∠ADB = ∠ADC
∴ ∆ADB ≅ ∆ADC
⇒ BD = DC
BD = DC =
1/2
BC
Since ∆ADB is a
right triangle right- angled at D.
∴ AB2 = AD2 + BD2
⇒ AB2 = AD2 + (1/2
BC)2
⇒ AB2 = AD2 +
BC2/4
⇒ AB2 = AD2 + AB2/
4
⇒ 3/
4
AB2 = AD2
⇒ 3AB2 = 4AD2
OR
Solution 25 .
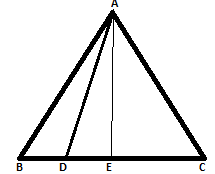
AE ⊥ BC
In ∆AEB and ∆
AEC, we have
AB = AC
and, ∠B = ∠ C
∴ ∆AEB ≅ ∆AEC
⇒ BE = CE
Since ∆AED and ∆ABE are right triangles right-angled at E.
AD2 = AE2 + DE2 and AB2 = AE2 + BE2
AB2
- AD2 = BE2 - DE2
AB2 - AD2 = (BE + DE)(BE - DE)
AB2 - AD2 = (CE + DE)(BE - DE)
AB2 - AD2 = CD . BD
Hence, AB2 - AD2 = BD . CD
Solution.26
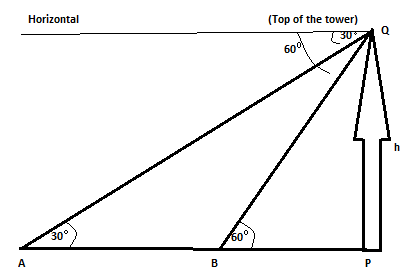
Let P be the foot of the vertical tower PQ of height h metres. Let the speed of the car be v m/sec.
At A the angle of depression of the car is 30o and six seconds later it reaches to B where the angle of depression is 60
o.
Clearly , car travels distance AB in 6 seconds with speed v m/sec.
∴ AB = 6v metres
Suppose car takes t seconds to reach to P from point B . Then , BP = vt metres .
∴ AP = AB + BP
= 6v + vt
In ∆ APQ , we have
tan 30o =
PQ/AP
1/√3
=
h/6v + vt
√3h = 6v + vt ---------(i)
tan 60o =
PQ/BP
√3 =
h/vt
√3 vt = h -----------(ii)
From i and ii, we have
√3 x √3 vt = 6v + vt
3 vt = 6v + vt
2 vt = 6v
t =
6v/2v
= 3 seconds
Hence, further time taken by the car to reach the foot of the tower is 3 seconds .
Solution.28
| Class interval: |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
∑f1 = 60 |
| No. of students: |
5 |
x |
20 |
15 |
y |
5 |
| Cumulative frequency (cf) |
5 |
5 + x |
25 + x |
40 + x |
40 + x + y |
45 + x + y |
We have
Median = 28.5
Clearly, it lies inthe class interval 20-30 . So,20-30
is the median class .
l = 20, h = 10 , f = 20 , F = 5 + x and N = 60
Now, Median = l +
x h
28.5 = 20 +
30 - (5 + x)/20
x 10
28.5 = 20 + 25 - x/
2
8.5 = 25 - x/
2
⇒ 25 - x = 17 ⇒ x = 8
We have , N = 60
∴45 + x + y = 60 ⇒ x + y = 15
Putting x = 8 in x + y = 15, we get y = 7
x = 8 and y = 7
Solution.29
Volume of water that flows per hour = (1540 x 60)litres
= (1540 x 60 x 1000)cm3--------------1
Inner diameter of pipe = 14 cm
Inner radius of pipe = 7 cm
Let h cm be the length of the
cylindrical column of water that flows in one hour .
Volume of water that flows in one hour
=
22/7
(7)2 x h cm3
-------------------2
now equating 1 and 2 , we get
22/7
(7)2 x h = 1540 x 60 x 1000
h = 600,000 cm = 6 km
Hence , the rate of flow of water is 6 km per hour .
Solution.30
secθ + tanθ = p ----------(i)
sec2θ - tan2θ = 1
(secθ + tanθ)(secθ - tanθ) = 1
p(secθ - tanθ) = 1 ⇒ secθ - tanθ =
1/p
--------(ii)
Adding and Subtracting i and ii
, we get
(secθ + tanθ) + (secθ - tanθ) = p + 1/p
and , (secθ + tanθ) - (secθ - tanθ)= p - 1/
p
⇒ 2secθ = p + 1/
p
and 2tanθ = p - 1/p
secθ = 1/2
(p + 1/p
) and tanθ =
1/2
(p -
1/p
)
Now, sinθ = tanθ/secθ
⇒ sinθ = 1/2
(p -
1/p
)/
1/2
(p +
1/p
)p2 - 1/p2 + 1





