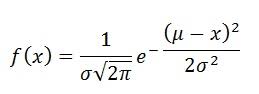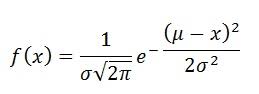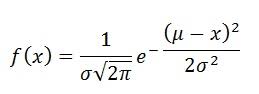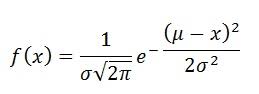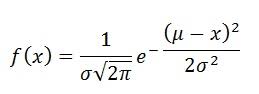FOLLOW US:

Question

Q1. Find the parameters of Normal Distribution whose p.d.f is -

f(x) =

1/9√(2π)

e^{(-1/162)(x - 12)2}

(a) (12,81)

(b) (12,12)

(c) (12,9)

(d) (12,4)

Solution.
parameters of normal distribution is x ∼ N (μ , σ²)

compare the given p.d.f with



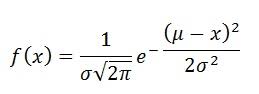
So in the case σ = 9 , μ = 12

x ∼ N (12,81)

Q2. Find the parameters of Normal Distribution whose p.d.f is -

f(x) =

1/√(18π)

e^{(-1/18)(x - 5)2}

(a) (1,1)

(b)(0,1)

(c) (5,9)

(d) (4,5)

Solution. c
parameters of normal distribution is x ∼ N (μ , σ²)

compare the given p.d.f with



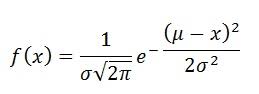
So in the case σ = 3, μ = 5

x ∼ N (5,9)

Q3. Find the parameters of Normal Distribution whose p.d.f is -

f(x) =

1/√(2π)

e^{(-1/2)(x2 - 4x + 4)}

(a) (1,1)

(b) (2,1)

(c) (2,2)

(d) (0,1)

Solution.b
parameters of normal distribution is x ∼ N (μ , σ²)

compare the given p.d.f with



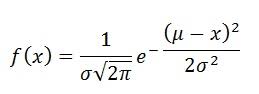
So in the case σ = 1,(x² - 4x + 4) = (x - 2)² , μ = 2

x ∼ N (2,1)

Q4. Find the parameters of Normal Distribution whose p.d.f is -

f(x) = constant . e^{-(x2 - 12x + 36)}

(a) (1/2 ,6)

(b) (6,1)

(c) (6,0)

(d) (6,1/2)

Solution.d
parameters of normal distribution is x ∼ N (μ , σ²)

compare the given p.d.f with



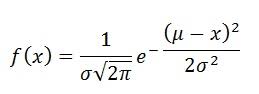
In this case constant =

1/σ√(2π)

-

1/2σ²

= -1

σ² =

1/2

σ = √(

1/2

)

μ = 6

x ∼ N(6,1/2)

Q5. Find the parameters of Normal Distribution whose p.d.f is -

f(x) = constant . e^{-(1/8)(x2 - 2x + 1)}

(a) (1,4)

(b) (2,3)

(c) (0,1)

(d) (4,1)

Solution.a
parameters of normal distribution is x ∼ N (μ , σ²)

compare the given p.d.f with



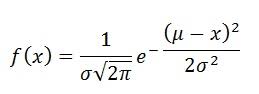
In this case constant = -

1/2σ²

= -

1/8

1/σ²

=

1/4

σ = 2 and (x² - 2x + 1) = (x - 1)²

μ = 1

x ∼ N(1,4)